Aurei visivi

“Il tutto sta alla parte come la parte sta al rimanente”

Parliamo della sezione aurea, uno dei valori più interessanti per chiunque si occupi di bellezza, di grafica, di comunicazione visiva, di arti figurative, di progettazione, e di esseri umani.

La sezione aurea o rapporto aureo o numero aureo o costante di Fidia o proporzione divina, indica il numero irrazionale 1,6180339887... Questo numero, come vedremo, assolutamente speciale è chiamato anche Phi. Da dove viene questo numero? Questo valore discende dal rapporto fra due lunghezze, tra loro disuguali; discende dal rapporto tra due segmenti (segmento a e segmento b) ed una linea (linea l) lunga quanto la somma dei due segmenti (a+b).

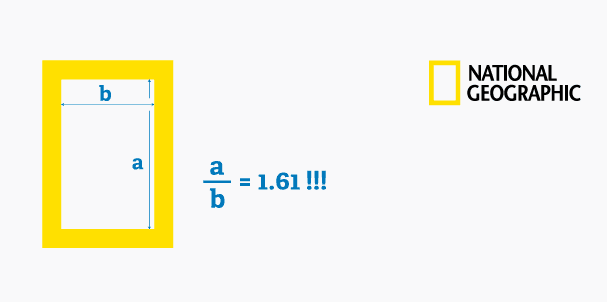
In altri termini, considerando una linea divisa su due parti diseguali, il rapporto tra la linea e la sua parte più grande è proporzionale tra la parte più grande e quella più piccola: la parte più corta (b) sta alla più lunga (a) come questa (a) sta all’intera linea (l=a+b) cioè b : a = a : l.
La maggiore a è medio proporzionale tra la minore b e la somma delle due (a+b).

Che ce ne frega?

Ce ne fregherebbe non moltissimo se quel valore non fosse così visivamente interessante, così immensamente presente nella natura, e così determinante nella percezione di ciò che consideriamo esteticamente bello.

Cerchiamo di capirci, non tutti i rettangoli ci sembrano belli alla stessa maniera: alcuni li consideriamo troppo allungati, altri troppo schiacciati, etc. Perché? Cosa significa troppo? E troppo rispetto a che cosa? Quale è il "senso estetico" che portiamo dentro di noi, da cui non possiamo divergere "troppo"?

Consideriamo belli quei rettangoli il cui lato lungo sta in proporzione al lato corto come la somma dei due sta al lato lungo. Ci piacciono i rettangoli che hanno valori aurei.

Non è vero?

Il monitor, il tuo cellulare, la tv che hai a casa, il portafogli che tieni in tasca, il tuo block notes, ma anche il tuo quaderno, il libro che preferisci, il foglio della stampante e la cartelletta in cui li conservi, la tessera della banca, i tuoi bellissimi bigliettini da visita, le ante del mobile della cucina, l'edizione cartacea del quotidiano ed anche il magazine allegato, la confezione del tuo amato gioco da tavolo, la cassetta della frutta, il porta documenti per l'assicurazione dell'auto, il fronte dello scatolo di cartone della confezione di pastina per i bambini, lo strofinaccio, la scatole dei preservativi, la bandiera della nazionale, e la tessera del circolo dell'uncinetto sono tutti rettangoli. Non rettangoli qualsiasi, ma rettangoli aurei, in proporzione Phi.

Significa cosa?

Significa che ci piacciono le proporzioni auree, e che le riproduciamo in continuazione, costantemente, in maniera consapevole o inconsapevole, negli oggetti che produciamo.
Queste creazioni umane che sentiamo essere belle le generiamo anche nell'arte, pittura, composizione, computer grafica, architettura.
Il più grande scultore e progettista del passato è stato Fidia, che era conosceva ed usava consapevolmente il valore Phi per creare opere che fossero percepite come armoniose, valide, belle. Usava in continuazione questa proporzione, ed è il motivo per cui il valore aureo viene detto anche valore di Fidia.
Una enormità di artisti hanno usato, ed usano, il valore Phi nelle loro opera in maniera consapevole o meno.

Questa percezione è solo degli umani?

No. La risposta è no. Phi non è un valore che risponde esclusivamente ad una percezione umana. Si tratta di qualcosa di infinitamente più ampio e meraviglioso.

Per comprendersi serve una minuscola digressione: la successione aurea, o successione di Fibonacci (dal nome del matematico italiano che la individuò e diffuse) è una infinita successione di numeri in cui il rapporto di ciascuno elemento con il precedente produce un valore aureo Phi.

I primi 25 numeri dell'infinita successione di Fibonacci sono: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,144, 233, 377, 610, 987,1597, 2584, 4181, 6765,10946, 17711, 28657, 46368, 75025. 

Seguendo la seguente unica regola ricorsiva:

F_{0}=0,
F_{1}=1,
F_{n}=F_n-1+F_{{n-2}}  Per ogni n>1

Il rapporto tra ciascun numero della serie ed il precedente genera un rapporto aureo.

La successione di Fibonacci è circondata da una fascinosa aura di mistero e ha suscita attenzione da ambiti lontanissimi dalla matematica. Perché? Perché descrive delle quantità, delle regolarità presenti e facilmente osservabili nei fenomeni naturali di crescita.
I numeri di Fibonacci ed i loro rapporti aurei sono rinvenibili nella disposizione delle foglie lungo un ramo di una pianta, nella forma dei fiori, nella quantità dei petali, nel numero delle spine, nella disposizione della materia, nella forma delle strutture ossee, all'interno dei fenomeni acustici e di riconoscimento di onde sonore, persino nel corpo umano, nelle forme generate dal movimento dei corpi vivi e non vivi.

Cos'è quella questione dei rettangoli e spirali?

Ecco. Si... C'è ancora un fatto interessante che ci aiuta a passare dai numeri agli aspetti visivi e corporei. La spirale aurea è un tipo particolare di spirale logaritmica con fattore di accrescimenti b di crescita pari a φ, la sezione aurea. Parlando in maniera più semplice?
La relazione tra i numeri di Fibonacci e la spirale logaritmica si rivela evidente se si costruisce una serie di quadrati in cui il lato di ognuno di questi è dato dalla somma delle misure dei lati dei due precedenti. Se li disponiamo come in figura e tracciamo un arco di cerchio avente per raggio il lato del quadrato, la figura che si ottiene è una spirale logaritmica.

La spirale logaritmica è intimamente legata ai numeri di Fibonacci, in cui ogni termine è dato dalla somma dei due precedenti. La sua esistenza è nota dal 1202.

A cosa ci serve e dove la troviamo questa spirale aurea?

La risposta è visiva.

I rapporti aurei, i rettangoli aurei, la spirale aurea, ed in generale i numeri aurei (serie di Fibonacci) sono presenti nella natura in maniera evidente e strabordante. Ne sono portatori i fenomeni atmosferici, la parte più intima della materia, così come i fenomeni stellari.

In natura dove sono ulteriormente visibili questi aspetti?

La risposta è ancora visiva.

Questi valori, queste proporzioni sono note anche a chi si occupa di arti grafiche. Ne sono coscienti i pittori, ma anche i grafici.

Qui alcuni loghi noti con valori aurei.